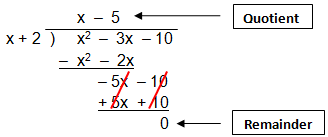Polynomial Division Problems That Have Nonzero Remainders
To set up the problem first set the denominator equal to zero to find the number to put in the division box. Furthermore there exist polynomials ux and vx such that dx fxux gxvx.
Math Help Algebra Synthetic Division Technical Tutoring
Euclidean division of polynomials is very similar to Euclidean division of integers and leads to polynomial remainders.

Polynomial division problems that have nonzero remainders. Enter the expression you want to divide into the editor. Let rx be the remainder when the polynomial x135x125-x115x51 is divided by x3-x. Divide the leading term of the obtained remainder by the leading term of the divisor.
Would like some help solving this. Divide 2x5 x46x9 2 x 5 x 4 6 x 9 by x2 3x 1 x 2 3 x 1 Solution. Rx is a nonzero constant c.
We can find the quotient qx and the remainder rx by performing ordinary long division with polynomials. Use the division algorithm to divide polynomialsPolynomial division and rational expressions playlist. Finally subtract and bring down the next term.
The degree of rx is one d. Next make sure the numerator is written in descending order and if any terms are missing you must use a zero to fill in the missing term finally list only the coefficient in the division problem. Theorem 1 The Division Algorithm for polynomials.
Steps 2 3 and 4. In algebra the greatest common divisor frequently abbreviated as GCD of two polynomials is a polynomial of the highest possible degree that is a factor of both the two original polynomials. For example x²-3x5x-1 can be written as x-23x-1.
The most common method for finding how to rewrite quotients like that is polynomial long division. In this case we should get 2x 3 2x x 2 and x 2 2x 3. How would I apply the remainder theorem.
Divide 2x3 9x2 15 by 2x 5. The problem is that we cant generally find a quotient q such that ϕ x q x ψ x without remainder. Any quotient of polynomials axbx can be written as qxrxbx where the degree of rx is less than the degree of bx.
Its a expression on the form. Given two univariate polynomials ax and bx where bx is a non-zero polynomial defined over a field in particular the reals or complex numbers there exist two polynomials qx the quotient and rx the remainder. - 5 xleftx-7right- 5 x235 x.
Divide 3x4 5x2 3 3 x 4 5 x 2 3 by x2 x 2 Solution. Theorem 2 The Remainder Theorem for polynomials. Divide x32x23x4 x 3 2 x 2 3 x 4 by x7 x 7 Solution.
This concept is analogous to the greatest common divisor of two integers. In the long division I divided by the factor x 3 and arrived at the result of x 2 with a remainder of zero. Arrange the coefficients in the apt order and perform the usual process to arrive at the quotient and the non-zero remainder.
This latter form can be more useful for many problems that involve polynomials. Q is the quotient and r is the remainder. Polynomial long division with no remainder.
In my post Polynomials Division by Vision I presented a. The polynomial division calculator allows you to take a simple or complex expression and find the quotient and remainder instantly. As you can see above while the results are formatted differently the results are otherwise the same.
Multiply it by the divisor. Then there exists a unique gcd dx of fx and gx. Click the blue arrow to submit and see the result.
First off I note that there is a gap in the degrees of the terms of the dividend. For problems 1 3 use long division to perform the indicated division. This means that x 3 is a factor and that x 2 is left after factoring out the x 3Setting the factors equal to zero I get that x 3 and x 2 are the zeroes of the.
ϕ x q x ψ x r x this is the general form that the long division algorithm processes. A fresh way to apply division by vision in higher order polynomials with quadratic quotients with remainders while saving time. My work might get complicated inside the division symbol so it is important that I make sure to leave space for a x.
Enhance your skills of dividing polynomials using synthetic division with these printable worksheets. Frac- 5 x2x- 5 x. Its existence is based on the following theorem.
If the polynomial px is divided by x a then the remainder. Divide the term with the highest power inside the division symbol by the term with the highest power outside the division symbolNext multiply or distribute the answer obtained in the previous step by the polynomial in front of the division symbol. If the polynomial px is divided by dx then there exist polyno-mials qxrx such that pxdxqxrx and 0 degreerx degreedx.
Write down the calculated result in the upper part of the table. Section 5-1. The polynomial 2x3 9x2 15 has no x term.
The degree of rx is two. In the important case of univariate polynomials over a field the polynomial GCD may be computed like for the. Dividing Polynomials Using Synthetic Division With Remainder.
Let F be a eld fxgx 2Fx not both 0. Rx is the zero polynomial b. It the last nonzero remainder has to be multiplied by a constant to make it monic For variety we shall follow the books proof this time.
I M Struggling With Polynomial Division Long Division Seems Like A Dirty Trick That Requires A Lot Of Memorization And My Teacher Doesn T Know Why It Works Is There A Deeper Way To
Openalgebra Com Synthetic Division

Use Synthetic Division To Divide Polynomials College Algebra
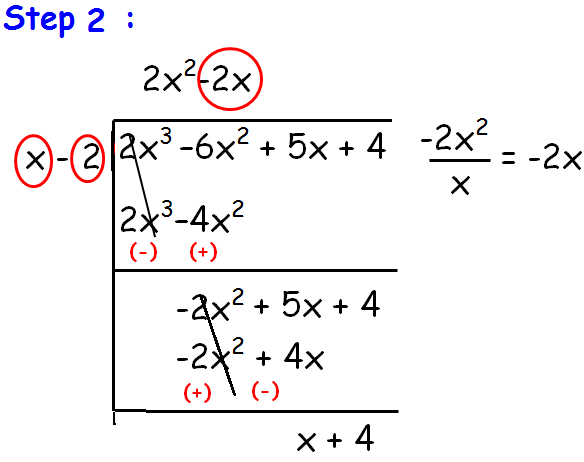
Dividing Polynomials Using Long Division

4 4 Dividing Polynomials Mathematics Libretexts

Dividing Polynomials Algebra And Trigonometry

Dividing Polynomials College Algebra
Openalgebra Com Dividing Polynomials

Dividing Polynomials With Long Division No Remainder Youtube
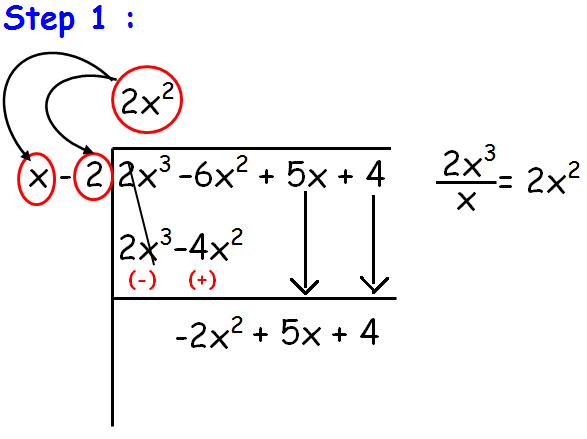
Dividing Polynomials Using Long Division

Dividing Polynomials College Algebra

Use Long Division To Divide Polynomials College Algebra

Polynomial Division Brilliant Math Science Wiki

Dividing Polynomials Worksheets

Long Division Of Polynomials Tips Tricks Examples Cuemath

Polynomial Division Brilliant Math Science Wiki